MMA 的不完全指南

凉凉

~~MMA (Mixed martial arts, 中文名称综合格斗), 并不是所要介绍的东西.~~

(免责声明: 你说的对, 但是 |\/|ATHE|\/|ATIC/\ 是一款缩写为 MMA 的, 中文翻译为综合格斗的东西. 如果因为我拼写错误造成了网页链接到了奇怪的地方提供了奇怪的 MMA 的安装包的话, 那么纯粹只是二进制的随机组成, 其产生原因只是宇宙射线对我的键盘上的芯片触点的未知影响, 不代表我个人的任何意志.)

如何下载 Mathematica

这是摘录 Wolfram 官方的邮件的部分内容:

If you need to download your product from the Wolfram User Portal, go to: https://user.wolfram.com.
If you do not have a Wolfram ID to sign in to the Wolfram User Portal, you can create one. Please use xxxx@mails.ucas.ac.cn (注: 这里我码掉了我自己的邮箱) as your Wolfram ID to access your product download.

请前往 user.wolfram.com 并登陆以学校邮箱为用户名的 Wolfram 账号,
你应该可以看到有 Mathematica 的 Product and Service,
点击 Get Download 超链接,
然后在 Mathematica Chinese Edition for Students for Sites 这个页面, 拉到最下方
选择 Direct File Download (这不会用 Wolfram 的那个鸡肋下载器下载, 而是直接下载完整安装包)

Image description

如何安装 |\/|ATHE|\/|ATIC/\

一个关于如何安装 MMA 的网站. 并且总所周知, MMA (综合格斗) 是一个小圈子, 不像隔壁 MatLab (Multiply and Add To Lab, 乘法加法工作室) 那么被广泛传播. 可能是因为 MMA 的注册机制基本没有更新过吧.

更新: 14.1 及以后的注册机制可以见 Aluria 的网站.

免责声明: 大家应该只是因为校园网太烂连不上 Wolfram 的注册机制所以不得以使用注册机的吧.

凉凉无关的一个感慨:
如果我们学校的数理课程可以引入计算机代数系统来辅助的话就好了,
上网查资料的时候看到复旦的一个课程就是通过 Mathematica 来讲数学物理方法. (链接)

凉凉

MMA 和机器学习

因为去次修了一门模式识别和机器学习, 作业里面需要搞点机器学习的东西, 尝试安利 MMA, 然而失败.

MMA 的话, 实际上确实可能并不是那么的出名, 甚至你可能没准压根就没有听过 MMA 是什么.

凉凉你说的对, 但是 |\/|ATHE|\/|ATIC/\ 是一款缩写为 MMA 的, 中文翻译为综合格斗的东西.

简单的机器学习的函数

我认为 MMA 的函数对于简单的问题非常的好用, 或者说有点近似于无脑调用了的情况了. 比如说要解决分类问题, 并且使用的是 NaiveBayes 方法. (别问我为什么用这个方法, 只是它目前看来挺靠谱的).

Image description

实际上也可以直接不指定方法, 直接让 MMA 为你选择, 并且最后可以使用 Information 的形式来读取训练得到的函数的信息:

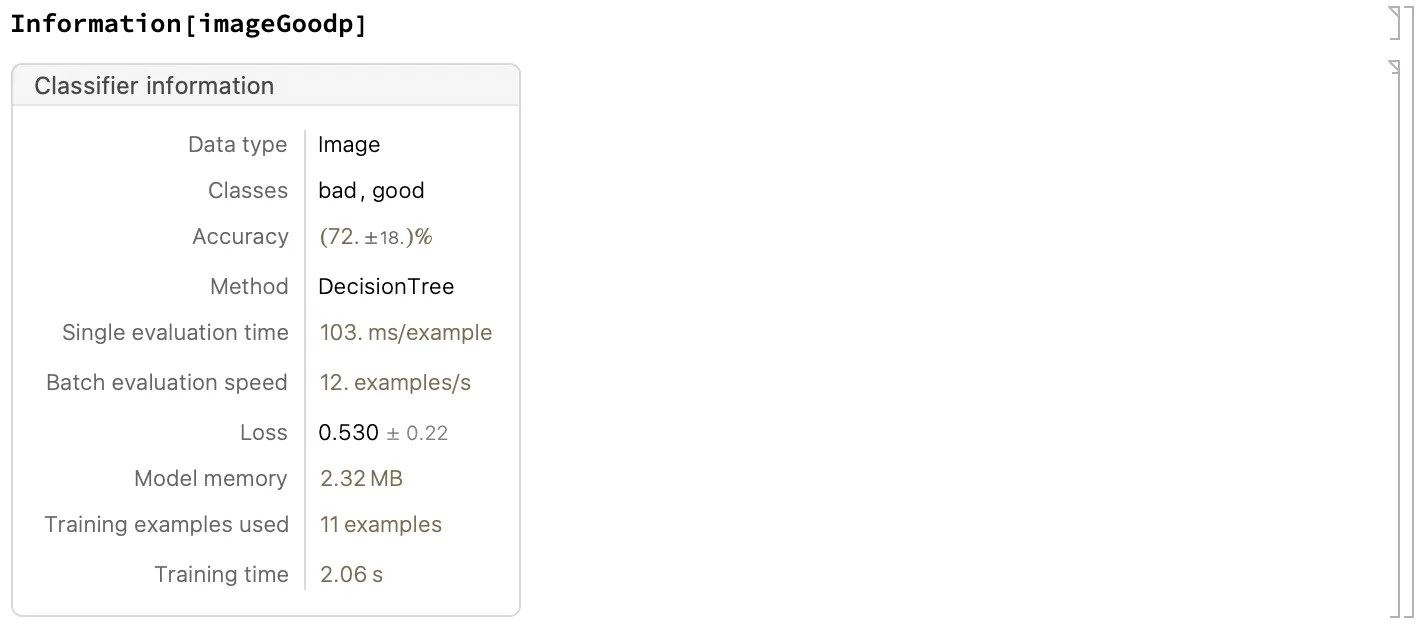
Image description

众所周知, 模式识别中有两种问题: 分类和回归. 而说得更加玄学一点, 就是假设现实问题中真的存在这样的一个 $F(x)$, 使得输入和结果存在一定的关系. 而最终的目标就是在一个样本集的基础上 ${x \rightarrow F(x) + \mathrm{noise}}$ 希望找到一个 $f(x)$ 使得其尽可能地接近 $F(x)$. 至于分类和回归问题, 那么就是 $f(x)$ 的像空间是连续的, 还是离散的 (尽管
大部分时候这两个问题没法区分).

那么教练, 我想试试看回归模型: 在 MMA 中使用 Predict 命令即可进行回归操作.

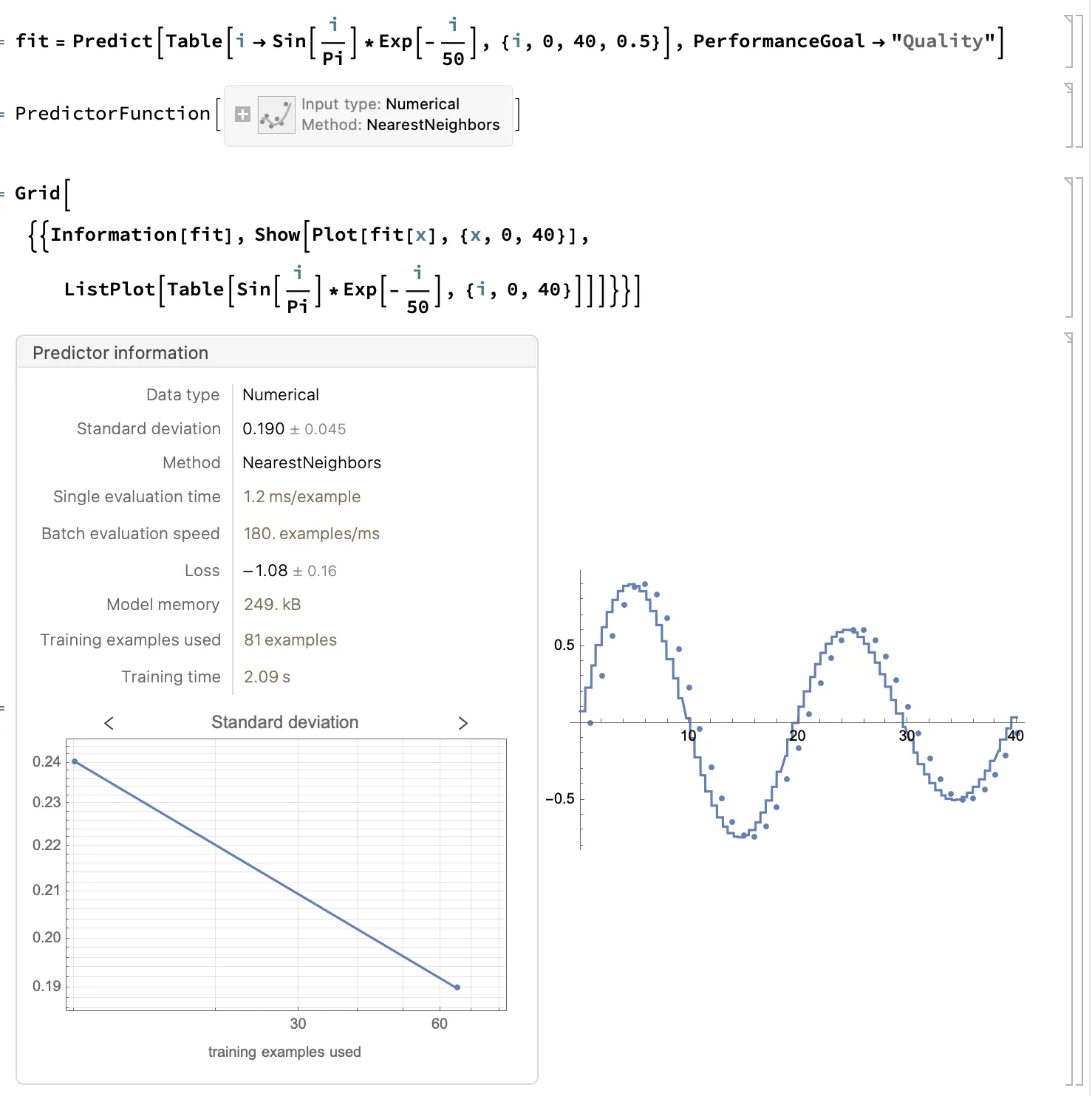
Image description

尴尬, 这样拟合的函数效果并不是很好💦.

(注: 如果是想要根据函数分布来猜出函数的解析表达式的话, 实际上可以尝试 FindFormula, 不过最终的效果并不一定很好. ~~实际上大部分的情况下都是这样的, 虽然大部分情况下, 这些函数很好用, 但是并不是万能的, 经常会打脸...~~. 如果对解析解非常好奇的话, 有一个项目可以看看: PhySO | Github, PhySO | arxiv)

当然, 还有聚类函数 Cluster 之类的比较通用一些的分类函数. 这里就不一一展开了. 如果想要提高准确率的话, 可以考虑使用 LinearRegression, LogisticRegression 等等的一些更加细致一些的函数.

这样是不是有点不太够呢?

如果你想要更加细致的, 更加 “实用” 一些的机器学习框架, 不妨来考虑一下使用 MMA 提供的网络仓库, 里面集成了一些比较常见的神经网络. (并且可以直接在线运行, Basic版本的 Wolfram Cloud 虽然很 low, 但是也不是不能用:

比如以瑟瑟图片检测网络 (Yahoo Open NSFW Model V1) 来作为一个例子 (在 Wolfram Cloud 上跑的):

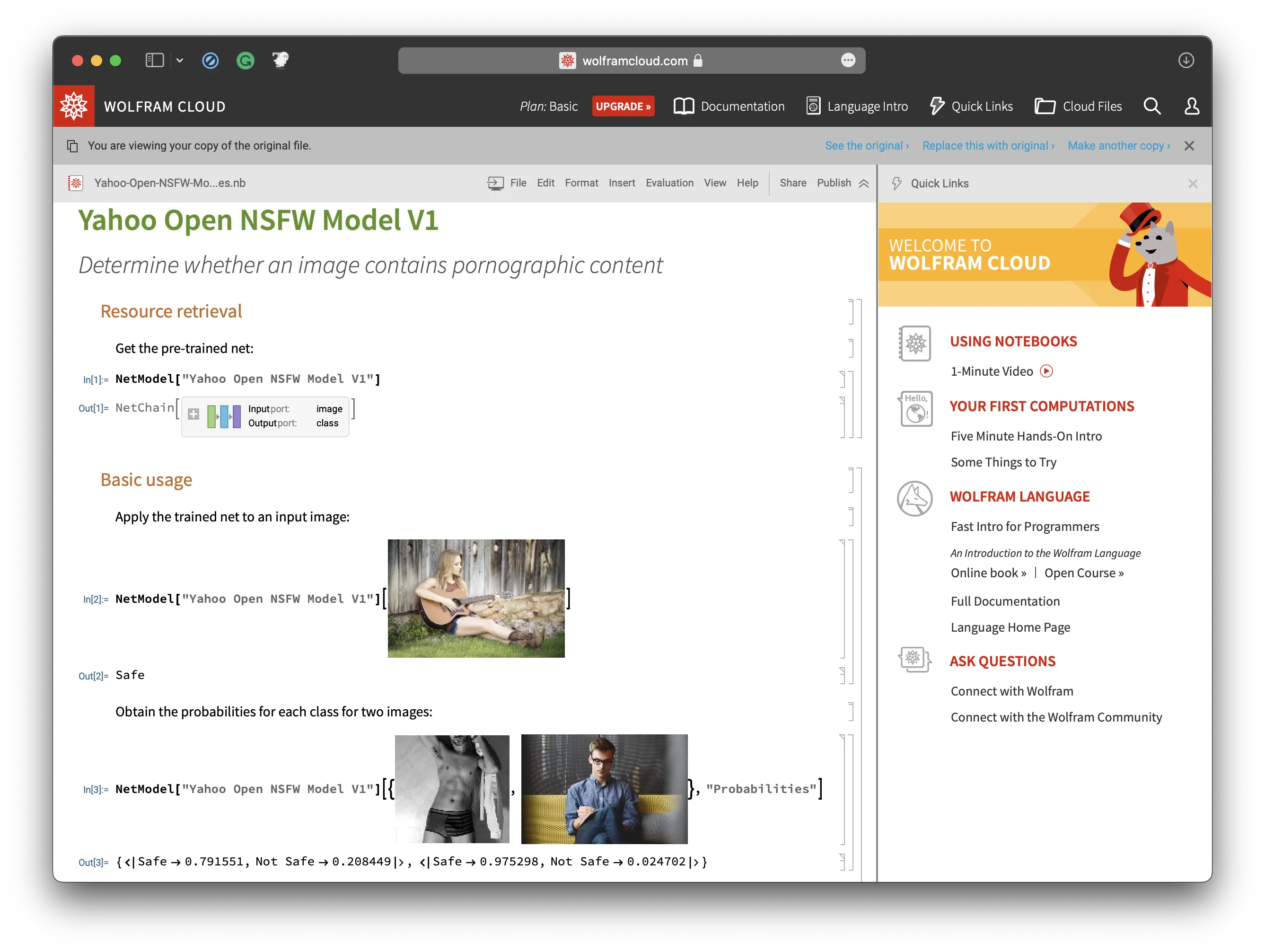
Image description

~~冷知识: NSFW 的全称是 Not Safe For Work. 所以作为一个正直的青年, 我只能展示一点点, 具体可以自己试试.~~

能不能再上点强度?

使用 Information[NetModel["Yahoo Open NSFW Model V1"], "SummaryGraphic"] 可以提取并观察一个神经网络的具体构建方式, 里面有各种各样的层, 那么实际上自己通过层开始进行一个网络的构建也不是不可以:

比如说最简单的一个线性的层, 将五个参数整合在一起:

uninitializedNet = NetChain[{LinearLayer[1, "Input" -> 5]},
  "Input" -> 5,
  "Output" -> 1]

以及构造用于训练的网络:

trainingNet = NetInitialize@NetGraph[<|
    "linear" -> uninitializedNet,
    "loss" -> MeanSquaredLossLayer[]|>,
   {NetPort["Input"] -> "linear" -> NetPort["loss", "Input"],
    NetPort["Target"] -> NetPort["loss", "Target"]}]

其中, 损失函数为 MeanSquaredLossLayer, NetInitialize 给整个网络中的未确定的参数进行随机赋了一个初始值. (注: 如果有那种预训练的网络的话, 你可以理解为预训练相当于给了一个比较好的初始值, 可以有助于训练结果快速收敛)

于是构造一堆数据用来训练:

data = Association[
   Flatten[Table[{x1, x2, x3, x4, 
       x5} -> {2 x1 + 3 x2 - 4 x3 + 5 x4 - 5 x5 + 1 + RandomReal[0.1]},
     {x1, -2, 2}, {x2, -2, 2}, {x3, -2, 2}, {x4, -2, 2}, {x5, -2, 2}],
     4]];

(* 数据的格式如下 *)
RandomSample[data, 5]
(* <|{0, -1, -1, 1, 1}   -> {1.32546}, 
     {1, 1, 0, 1, 1}     -> {5.19757}, 
     {0, -1, -2, -1, -2} -> {10.3261}, 
     {1, -2, -2, 0, 2}   -> {-5.15193}, 
     {-2, 0, 1, 2, -2}   -> {12.8819}|> *)

简单粗暴地划分一下训练集和测试集并喂给训练的网络去进行训练. (注: 一开始 RandomReal 的噪声加大了, 没法消除. )

With[{first = data[[1 ;; -1000]], last = data[[-1001 ;; -1]]},
 trainData = <|"Input" -> Keys@first, "Target" -> Values@first|>;
 testData = <|"Input" -> Keys@last, "Target" -> Values@last|>;]

results = NetTrain[trainingNet,
  trainData, All, ValidationSet -> testData, MaxTrainingRounds -> 320];

从最终的结果中提取训练好的那部分网络并对其进行检测判断:

trainedNet = NetExtract[results["TrainedNet"], "linear"];
testF = Function[{x1, x2, x3, x4, x5}, {2 x1 + 3 x2 - 4 x3 + 5 x4 - 5 x5 + 1}];

(trainedNet[#] - testF @@ #) & /@ {
  {1, 0, 0, 0, 0}, {2, 3, 4, 5, 6}, {9, 9, 9, -9, -9}}
(* {{0.0483317}, {0.0473833}, {0.038662}} *)

还行吧.

能不能再进一步?

比如说我想要使用各种各样的 Layer 而不是仅仅只是 LinearLayer. 以及除了简单的单层 Layer, 还想要多层的 Layer, 想要网状结构的 Layer:

没问题, 可以使用 ?*Layer* 来查询所有包含 Layer 名字的函数, 于是就可以用其去构建更加复杂的网络.

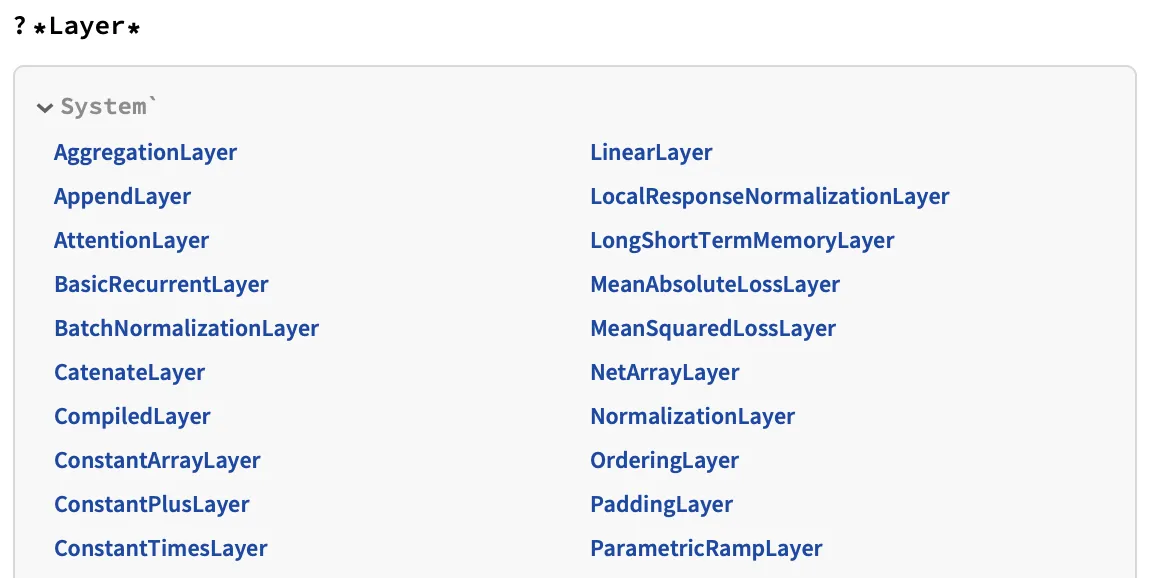
Image description

图片太长, 懒得截图了.

比如说可以构造一个 LeNet:

uninitializedLenet = NetChain[{
   ConvolutionLayer[20, 5],
   ElementwiseLayer[Ramp],
   PoolingLayer[2, 2],
   ConvolutionLayer[50, 5],
   ElementwiseLayer[Ramp],
   PoolingLayer[2, 2],
   LinearLayer[500],
   ElementwiseLayer[Ramp],
   LinearLayer[10],
   SoftmaxLayer[]},
  "Input" -> enc,
  "Output" -> dec]

其中 enc 和 dec 制定为输入和输出的处理器:

dec = NetDecoder[{"Class", Range[0, 9]}];
enc = NetEncoder[{"Image", {28, 28}, "Grayscale"}];

即 dec 为一个可行值为 0~9 的一个分类器, enc 将输入的图像变为 28x28 输入的灰度图像.

能不能再上点强度?

比如说想要自己编写层函数 FunctionLayer, 想要自己编写损失函数? 虽然好像也不是不行, 但是目前我还没有走到那一步. (简称: 没那个能力)

如果之后能更新的话再更新吧.

凉凉

阿伟, 你怎么又在看 MMA 了? 都说了多少次了, 不要老看电视, 要好好学习啊...
摘自《孟母劝学》

那么还是好好学习吧:

有键盘就行的复变函数

该栏涉嫌违反广告法, 因为实际上并不可以.
~~比如你不能在考试的时候... 除非有一天我能看到...~~

复数的运算

基本的运算和输入

打开一个 MMA 窗口, 输入: (默认的输入的样式是 Input, 如果你没有做什么会坑到自己的操作的话)

(1 + 2 * I)^4

然后按下 Shift-Enter, 即同时按下 Shift 键和 Enter 键(回车键). 就可以在输出看到 -7-24i (不过这个 i 是一个中空粗体的 i)

当然, 如果你想要输入一些特殊的符号 (特殊的 Unicode, 比如 π 之类的), 可以通过按下 ESC 键后, 再输入索引用的名字然后通过 ESC 退出. (不过因为会自动跳出来补全, 以及你可以通过 LaTeX 的方式进行索引, 比如: ESC \pi ESC 会得到 π, 不过也可以通过 ESC p ESC 来快速输入就是了. )

MMA有良好的 自动缩进换行(比如在正常使用的时候, 除非你是那种强迫症, 基本可以不用换行和考虑这些, 比如一大佬曾对我说: “难道MMA中有必要用空格 (对齐) 么? ”), 语法高亮 (比如在环境中有绑定的变量名字的颜色和未绑定的是不同的, 前者默认是黑色的, 后者默认是蓝色的)以及补全 (总之就是很爽).

广为人知的小技巧: MMA的数学公式实际上输入非常的方便. 你可以尝试按下 Ctrl-/ 键 (之后用 C-/ 来表示), 以及 C-^ (即按住 Ctrl 再按住 Shift 再按住 6, 如果你的键盘是正常的配列的话) 等等.

函数

在MMA中, 一个函数的调用可能如下所示: (其中 (* *) 为注释)

Abs[3 + 4 * I]       (* Out: 5 *)
Arg[1 + Sqrt[3] * I] (* Out: \[Pi]/3 *)

也可能是这样:

Re[Sin[15 * Degree]] // N (* Out: 0.258819 *)

即将前面的部分作为参数传递给下一个函数. (等价于 N[Re[Sin[15 * Degree]]], 写起来比较方便)

代数基本定理

农民版本: 多项式在复数域下有解, 可以分解为 $f(x) = \prod_i (z - z_i)^{\alpha_i}$ 的形式

定义多项式为 expf 为 $(z^{8} - 1)(z^{3} + 8)$, 通过 Factor 将其分解因式.

expf = (z^8 - 1) (z^3 + 8);
Factor[expf] (* Out: (-1 + z) (1 + z) (2 + z) (1 + z^2) (4 - 2 z + z^2) (1 + z^4)*)

(其中用分号结尾的语句不会输出到 Out 中)

在代数问题中, 如果你遇到了不好解决的问题, 不妨先将问题放到一个更大的域里面去解决. 然后再缩小域.
大致意思转述来自线性代数-B 韩阳老师班 (也有可能是助教魏大哥, 大概)

故, 在 MMA 中, 默认是在 $\mathcal{C}$ 中进行一个计算. 不过你也可以通过 Assuming 来限定运算所在的域或者添加其他的条件:

Refine[Sqrt[x^2]]                   (* Out: Sqrt[x^2] *)
Assuming[x > 0, Refine[Sqrt[x^2]]]  (* Out: x *)

极限与微积分

极限

Limit[Sin[x]/x, x -> 0] (* Out: 1 *)

注: 你可以用 MMA 试试看输入 -> 会发生什么.

上面的公式: 对于 $\frac{\sin x}{x}$ 来说, $x = 0$ 是一个可去奇点.

当然, 对于非奇点部分, Sin[x] / x /. x -> 5 会得到 Sin[5] / 5. 其中 /. 表示将前面运算结果进行替换, 将 x 替换为 5. 当然可以通过 Sin[w * t] /. {w -> 2 * Pi, t -> 1} 来替换多个符号.

微分和积分

在 MMA 中, 所有的导数都可以认为是偏微分. ~~毕竟没什么区别.~~

D[1/(1 - z^2), z]

于是就可以检测 C-R 条件, 或者是调和函数: 其中使用 f[arg_<TYPE>] := <exp> 的方式来定义函数表达式, 使用 ; 在结尾来取消输出到 Out 中.

testCRCondition[u_, v_] := 
  And[D[u, x] == D[v, y], D[u, y] == -D[v, x]];
testCRCondition[x^2 - y^2, 2*x*y] (* Out: True *)

testHolomorphic[f_] :=
  Assuming[x \[Element] Reals && y \[Element] Reals,
   D[f, {x, 2}] + D[f, {y, 2}] == 0];
testHolomorphic[(x + I*y)^2]
testHolomorphic[Re[x + I*y]]

于是对于一个简单的调和函数, 可以求得其对应的 "另一半":

expu = Exp[x] Sin[y];
testHolomorphic[expu] (* Out: True *)

确认过为调和函数, 使用 C-R 条件计算得到:

expDvDx = D[expu, y];
expDvDy = -D[expu, x];

再利用普通的路径积分即可得到:

Integrate[expDvDx, x];
expv = Integrate[expDvDy - D[%, y], y] + % (* Out: Exp[x] * Cos[y] *)

其中 % 为上一次计算的结果. 同理还能用 %<Num> 来得到 Out[<Num>] 的结果.

虽然一般更喜欢用这种方式:

DSolve[{
  D[v[x, y], x] == expDvDx,
  D[v[x, y], y] == expDvDy
  }, v[x, y], {x, y}]
(* Out: {{v[x, y] -> C[1] + E^x Cos[y]}} *)

幂级数展开

算一个级数: 在原点展开到5次项

Series[Exp[z], {z, 0, 5}]
(* Out: SeriesData[z, 0, {1, 1, 
Rational[1, 2], 
Rational[1, 6], 
Rational[1, 24], 
Rational[1, 120]}, 0, 6, 1] *)

(输出逐渐变得不太方便表示了... )

对于洛朗级数, 实际上可以看作是将 z -> 1/u 进行一个替换后再进行一个展开. (双边展开)
不过为何要如此繁琐呢?

Series[1/(z^2 (z - 1)), {z, 0, 2}]
(* Out: SeriesData[z, 0, {-1, -1, -1, -1, -1}, -2, 3, 1] *)

留数定理

柯西定理: 对解析函数有: $\oint_C f (z) \mathrm{d}z = 0$
留数定理: 构造一个回路绕开所有的瑕点, 对瑕点特殊关照一下, 做一个半径无穷小的一个回路包围瑕点, 该回路的积分即洛朗级数的 $a_{-1}$ 项. 于是可以得到留数定理: $\oint_C f (z)\mathrm{d}z = 2\pi i \sum \mathrm{Res}(f(z_k))$
所有留数的和为 0, 这个可以用来计算本性奇点或者懒得算的奇点.
柯西公式: 在柯西定理的基础上, 构造有瑕点的 $\frac{f}{z - z_ 0}$ 表达式, 并通过留数定理即可知, 积分为 $f(z_ 0)$

FunctionPoles[Exp[z]/(1 + z), z]
Residue[Exp[z]/(1 + z), {z, -1}]

先写这么多, 之后再更.

(因为文件无法上传, 所以在最后用图片的形式来吧. )

MMA 的参考文档

哪里不会点哪里哦~
先生、これ何ですが？
うや！そこ、だめです！
摘自 “小天才一样的点读机” 广告

在 MMA 里面, 如果你是中文版本的话, 会在每个函数下面都用中文帮你翻译(解释)一下这个函数的功能. 或者你可以选择在弹出下面菜单栏一样的图标的时候按一下下键(或者那个向下的图标).

一个图标提示你可以展开

于是就可以展开一个快速帮助菜单:

展开的快速帮助

不过用的最多的应该是把光标移动到函数上, 然后按下 F1 按键打开对应的帮助文档.

Integrate的帮助文档

如果你也是一个会闲着没事上课看文档摸鱼的人的话, 那么基本上可以靠文档和搜索引擎自给自足了.

代码

代码传不上来, 那就之后补坑吧.

凉凉

凉凉
书接上回.

又: 完整版的代码在这里下载

留数定理

首先是找到函数的奇点:

FunctionPoles[Exp[z]/(1 + z), z]
(* Out: {{-1, 1}} *)

发现在 $z =-1$ 处有一个 1 阶奇点. 当然实际上在无穷远处还有一个本性奇点. 可以用留数和为 0 来得到.

Residue[Exp[z]/(1 + z), {z, -1}]
(* Out: 1/E *)

当然, 你可能也想要将这些函数整合在一起, 通过一个函数来调用. 那么这个时候, 你可能需要了解一些关于 MMA 中的一些类型以及对应的方法.
比如, 在上面的 FuctionPoles 的返回值, 用一个花括号括起来的是什么东西? 以及, 该怎么处理得到的这些东西?

首先, 在 MMA 中, 用一个花括号括起来的是一个 List:

List[1, 2, 3, 4]
(* Out: {1, 2, 3, 4} *)

你可以通过使用 Part 函数来得到一个 List 的第几个元素. 不过和一般编程不同的是, MMA的第一个元素就是是第一个元素. (不是第零开始的计数就是了)

{1, 2, 3}[[1]]
(* Out: 1 *)

当然, 与其用 For 历遍所有的元素, 不如通过 Map 来对一个列表进行处理:

funcPolesAndRes[f_, z_] := Map[
   ({#[[1]], Residue[f, {z, #[[1]]}], #[[2]]}) &,
   FunctionPoles[f, z]];
funcPolesAndRes[z/((z - 1) (z - 2)^2), z]
(* Out: {{2, -1, 2}, {1, 1, 1}} *)

其中, (...)& 的形式构造了一个匿名函数, 通过 # 来访问传入的参数. 这样的匿名函数的好处就是方便:

Table[i, {i, 0, 5}] (* Out: {0, 1, 2, 3, 4, 5} *)
% // (#^2) &        (* Out: {0, 1, 4, 9, 16, 25} *)

傅立叶分析和拉普拉斯变换

傅立叶展开: 将函数扔到基底为三角函数的正交空间里面
傅立叶变换: 将函数变换到连续的频率空间里面 (感觉表达不严谨, 等一个数学系的来纠正)
拉普拉斯变换: 在傅立叶变换的基础上, 对于那些死不收敛的函数, 乘以一个收敛因子 $e^{-\sigma t}$ 后强制收敛, 然后进行傅立叶变换.

傅立叶分析

把一个函数展开成傅立叶级数:

$f(x) = \frac{a_0}{2} + \sum a_k \cos \frac{k \pi x}{l} + b_k \sin \frac{k \pi x}{l}$

其中:

$a_k = \frac{1}{\delta_k l} \int_{-l}^l f(x) \cos \frac{k \pi x}{l}\mathrm{d}x$

$b_k = \frac{1}{l} \int_{-l}^l f(x) \sin \frac{k \pi x}{l} \mathrm{d}x$

其中, $\delta_k = 2 \mathrm{\ iff\ } k = 0 \mathrm{\ else\ } 1$.

(不知道公式能不能正常显示)

于是可以得到:

akOfFourier[f_, t_, k_, l_] :=
  1/(l*If[k == 0, 2, 1])
    Integrate[f*Cos[(k*\[Pi] *t)/l], {t, -l, l}];
bkOfFourier[f_, t_, k_, l_] :=
  1/l Integrate[f*Sin[(k*\[Pi] *t)/l], {t, -l, l}];

其中, 定义使用了一个 If 用来判断 k 是否为 0. 如果是零的话, 就输出 2, 否则为 1.

akOfFourier[Abs[Sin[x]], x, k, \[Pi]/2];
% // Assuming[k \[Element] Integers, Refine[#]] &
(* Out: -(4/((-1 + 4 k^2) \[Pi] If[k == 0, 2, 1])) *)
% // Assuming[k > 0, Refine[#]] &
(* Out: -(4/((-1 + 4 k^2) \[Pi])) *)

(这里建议还是看代码吧... )

当然, 如果你不想要编程的话, 可以用现成的函数:

FourierCosSeries[Abs[Sin[x]], x, 5]
(* Out: 2/\[Pi] - (4 Cos[2 x])/(3 \[Pi]) - (4 Cos[4 x])/(15 \[Pi]) *)
FourierSinSeries[x, x, 5]
(* Out: -2 (-Sin[x] + 1/2 Sin[2 x] - 1/3 Sin[3 x] + 1/4 Sin[4 x] - 
   1/5 Sin[5 x]) *)

傅立叶变换和拉普拉斯变换

将时域的函数变成频域的函数:

FourierTransform[HeavisideTheta[t], t, \[Omega]]
(* Out: I/(Sqrt[2 \[Pi]] \[Omega]) + Sqrt[\[Pi]/2] DiracDelta[\[Omega]] *)

当然, 不能少了逆变换:

FourierTransform[DiracDelta[t], t, \[Omega]];
InverseFourierTransform[%, \[Omega], t]
(* Out: DiracDelta[t] *)

注: 在 MMA 中, 自带的函数的命名(一般)都非常有规律.

同理还有拉普拉斯变换:

LaplaceTransform[Sinh[\[Omega]*t], t, p]
InverseLaplaceTransform[%, p, t]

Fin

并没有, 只是这部分写完了.

完整的代码参见这里

IridiumLINCH-SK

警报：大一新生请慎用Mathematica，因为其即使无编程思维也可使用且功能过于强大，可能导致你对其使用上瘾从而丧失自主计算耐心。层主曾因此考出线性代数I期中42的成绩，是我本科阶段单次考试最低分（

葡萄味的玉米

一定要更下去啊！

凉凉

注: 因为后文会解释的原因, 目前并没有一丁点🤏关于 FP 的东西, 你可以理解为标题欺诈. 之后会更新... ~~(先去庆祝考完打会游戏)~~
以及, 完整的代码会在全部写完之后放上去.

MMA 和 FP (0)

免责声明: 这个更像是我整理的学习 FP 的时候的笔记, 然后用 MMA 来重新表达一遍.
鉴于本人能力有限, 不一定准确.
~~注: 本人的所有解释都不是官方的正式定义, 完全是农民的自我理解.~~

什么是 FP

你说的对, 但是 FP 只是一种编程的范式, 和实际的语言并没有特别多的关系. 当然, 你也可以说某些语言在设计之初就是为了强调 FP, 比如 Haskell 之类的 Pure Functional Programming Language. 但是你不能说像 C 语言这样的东西不能做. ~~只是做起来会非常难受罢了~~

和状态有关的编程

和 FP 对应的还有很多的编程的概念, 比如可以先看看远处 JKD 的图灵机 (状态机):

TuringMachine[{
  {inverse, 1} -> {inverse, 0, 1},
  {inverse, 0} -> {inverse, 1, 1},
  {inverse, 2} -> {stop, 2, 0}},
 {inverse, {0, 1, 0, 1, 2}}, 5]

图灵机的状态图

害, 关于图灵机, 我们还是不多赘述了. 只要知道一个简单的感觉: 那就是像这样的东西, 有一个状态转移的感觉. 在一个状态下, 接受输入, 执行操作, 变换到下一个状态 (也有可能是变换到自己这个状态, 也就是不变. )

比如说可以有一个历遍一个 List 的状态机:

TuringMachine[{
  {index_, read_} :> {index + 1, read^2, 1}},
 {1, {1, 2, 3, 4, 5}}, 5]

当然, 你可以用更加熟悉的方式来写这段程序 (如果你熟悉 C 的话):

aList = {1, 2, 3, 4, 5}
For[i = 1, i <= 5, i++, aList[[i]] = aList[[i]]^2];
aList

其中, 这段代码通过修改状态量 i 来记录当前要处理的数据的位置, 通过修改 aList 来处理储存的数据.
(注: 如果你不知道这个是什么的话, 可以翻译成人话来说. 一开始, i 的值为 1, 如果 i <= 5, 那么执行 aList[[i]] = aList[[i]]^2 这条语句, 执行完后, i++, 即 i 的值增加 1. 然后反复执行直到条件不成立. )

不过不管怎么样, 还请有一个大概的感觉吧. 比如求和的时候就用

sumOfTotal = 0;
For[i = 1, i <= Length[aList], i++, 
  sumOfTotal = sumOfTotal + aList[[i]]];
Print[sumOfTotal] (* Out: 55 *)

还是一个状态 sumOfTotal 和 i 相互之间的一步步更新来实现的.

感觉有点跑偏了

等一下, 讲的是 FP, 但是讲了那么多别的玩意是怎么回事? 这样下去岂不是让别的概念根深蒂固在我的脑子里面了么?

~~确实, 这也是我为什么前面写了那么多的原因, 因为刹不住车了. (雾)~~

凉凉

凉凉书接上回

既然已经跑偏了, 不如索性就继续跑偏吧. 在 MMA 中有一个叫做万物皆可计算的概念噱头. 即通过符号处理和数据结构用一个符号来抽象表示的方法来提供一个强劲的计算能力:
流汗黄豆的计算
(你就说能不能算吧)

实际的实现可能是将符号和可以计算的值进行了一个绑定, 然后在计算的时候根据值 (符号) 来处理. 毕竟 MMA 符号处理能力比较强.

并且在 MMA 中, 各种类型的值也都能被计算. 比如常见的从一个 List 取值的操作:

listExample = RandomInteger[5, 5] (* {{2, 1, 3, 0, 2}, {1, 4, 1, 4, 1}, {3, 0, 1, 3, 4}, {5, 4, 4, 1, 
  4}, {4, 0, 1, 1, 3}} *)
listExample[[1]]                  (* {2, 1, 3, 0, 2} *)
listExample[[1 ;; -3]]             (* {{2, 1, 3, 0, 2}, {1, 4, 1, 4, 1}, {3, 0, 1, 3, 4}} *)
listExample[[1 ;; 4 ;; 2]]        (* {{2, 1, 3, 0, 2}, {3, 0, 1, 3, 4}} *)

可能会 Python 的对这种写法比较熟悉 (slice).

但是如果想要取每个元素中的奇数个元素, 如对于 {{1, 2}, {4, 5}}, 只要 {{1}, {4}}. 尽管可能会非常自然地想要写一个循环然后历遍每个元素 item, 取其部分 item[[1;;-1;;2]]. 但是还有另外一种选择:

selectOdd = #[[1 ;; -1 ;; 2]] &;
selectOdd /@ listExample

其中定义了一个叫做 selectOdd 的函数, 接受一个参数并返回参数的奇数部分. 其中 & 为定义一个函数的缩写, 其等价于用 # 表示输入的参数来书写的 Function.

selectOdd[Table[n, {n, 1, 10}]]

而 /@ 这个看起来很奇怪的符号是 Map 函数的缩写, 即展开写作:

Map[selectOdd, listExample]

也就是可以将函数作为一个输入的参数的值来进行计算.即函数也就是一个普通可计算的值, 和常见的数值等都是地位等价的东西. 于是可以用一串的函数来做成一个更大操作流, 譬如可以这样对选出来的值进行求和:

Total /@ selectOdd /@ listExample

或者是在计算的时候想要在之前的结果上继续施加函数:

1/(Sqrt[3] + I)^6 // Simplify // N

因为直观地来看, 函数就像是马里奥穿水管, 一个输入映射到一个输出. 于是编程就变成了如何巧妙弯水管的操作了. 而经过线性代数的拷打之后, 一个 "水管" 的输出还是一个 "水管" 也不是那么奇怪吧.

那么这么做有什么好处呢? 答案是可以不用考虑变量的状态, 即每个变量要么就是设定之后不再改变 (除非你发现写错了, 这里指的是在程序运行的时候不会被作为状态修改), 要么就是随用随弃的临时的变量. 于是你便可以完全不必追踪一个变量的状态的变化, 而只需要在这个函数的操作流中引出一端即可观察中间步骤是否出现问题. (实际并不一定这么爽就是了)

并且最重要的还是, 这样会比较快. 因为 MMA 中实现了各种函数来帮你完成操作 (并且这些函数的优化都十分惊人), 基本上你只需要像拼积木一样使用即可. 并且一个 (来自官方的) 更加嘲讽的建议: 除非你能够实现的方法是 MMA 中没有的或者是你实现的方法效率更高, 那么请优先使用现成的函数.

嗯, 所以弯弯绕绕, 现在终于被我生硬地弯回了和函数有点关系的东西了.

那么至此, 就当作是序言写完了吧.

Notebook 见 MMA-and-FP-Zero.nb

(注: 有兴趣的大佬可以尝试读一下 $\lambda$ 演算子的文章. 😢~~因为太难读了所以放弃了~~.

凉凉

MMA 和 Metropolis 算法

简单介绍 Metropolis 算法就是带条件随机游走:

从初始状态出发, 记当前状态为 $state$
使用 $gen(s) \mapsto s'$ 随机生成一个新的可能状态, 通过 $acc(s, s')$ 判断是否可能转移到下一个状态.
重复执行直到满足采样数要求.

(嘶, 这么说来好像热学课上讲的东西好像就是这个... 诶, 我都听了个锤子啊)

那么这个代码就非常好写了:

Sampling[init_, genF_, accF_, samples_, burnIn_] :=
  Module[{state = init, candidate = genF[init]},
   (*去掉前面 burnIn 个采样点*)
   Do[Until[accF[candidate, state], candidate = genF[state]], burnIn]; state = candidate;
   (*记录 samples 个采样点*)
   Table[Until[accF[candidate, state], candidate = genF[state]]; state = candidate, samples]];

以软物质物理课上讲的例子 (大概, 听得不是很清楚):

oneDU[state_]             := (state - 3)^2*(state + 10)^2; (* 随便掰的, 差不多得了 *)
oneDGen[state_]           := RandomReal[{-1, 1}] + state;
oneDAcc[state2_, state1_] :=
  With[{dE = oneDU[state2] - oneDU[state1], kT = 300 (* 随便掰的 *)},
   Or[dE < 0, RandomReal[] < Exp[-dE/kT]]];

可以用一个比较 low 的动画来演示一下:

oneDAni = Animate[Show[{
    Histogram[oneDat[[;; t]]],
    Graphics@{PointSize[0.02], Point[{oneDat[[t]], 0}]}
    }], {t, 1, 10000, 1}, AnimationRate -> 200]

(请不要吐槽这个演示的代码很丑)

Image description

并且这样写代码在修改的时候就更加方便了, 比如如果想要加入二维自由游走:

twoDU[state_] := 0;
twoDGen[state_] := 
  With[{vec = 
     Table[RandomReal[{-1, 1}], 2]}, (If[Norm[vec] != 0, 
      vec/Norm[vec], vec]) + state];
twoDAcc[state2_, state1_] :=
  With[{dE = twoDU[state2] - twoDU[state1], kT = 300},
   Or[dE < 0, RandomReal[] < Exp[-dE/kT]]];

twoDat = Sampling[{0, 0}, twoDGen, twoDAcc, 100000, 100];

twoDAni = Animate[Show[{
    DensityHistogram[twoDat[[;; t]]],
    Graphics[{PointSize[0.05], Point[twoDat[[t]]], 
      Line[twoDat[[;; t]]]}]}], {t, 1, 100000, 100},
  AnimationRate -> 1000, AnimationRunning -> True]

输出的效果大概就是这样:

Image description

MMA 的性能和代码优化

一开始用的代码是这样的:

ImportanceSampling[init_, genF_, accF_, samples_, burnIn_] :=
  Module[{
    samplesC = samples,
    burnInC = burnIn,
    states = {},
    state = init,
    candidate},
   While[samplesC > 0,
    candidate = genF[state];
    While[Not[accF[candidate, state]], candidate = genF[state]];
    AppendTo[states, candidate];
    state = candidate;
    If[burnInC > 0, burnInC--, samplesC--]];
   states];

那么跑一个相同的东西, 用的时间是这样的:

Timing[Sampling[0, oneDGen, oneDAcc, 100000, 100];]           (* {0.888991, Null} *)
Timing[ImportanceSampling[0, oneDGen, oneDAcc, 100000, 100];] (* {9.30457,  Null} *)

区别在于 Sampling 的代码里面, 比较多得用的是 Mathematica 内置的函数, 而 ImportanceSampling 里面用了很多的弯路去实现同样的一个功能.

凉凉并且一个 (来自官方的) 更加嘲讽的建议: 除非你能够实现的方法是 MMA 中没有的或者是你实现的方法效率更高, 那么请优先使用现成的函数.

嗯, 嗨, 这就是性能提升的关键了. 并且带来的另外一个好处就是让代码变短了.

Global 和 Local

上面的代码里面用的是 Module, 类似的还有 With, 之所以不直接使用变量, 除了 Module 和 With 可以让多行代码组织在一起, 另外的一个原因是因为代码里面的变量会变成局部 (Local) 变量, 这样就不用担心会污染到全局变量 (Global) 了.

~~虽然大多数情况下并没有什么鸟用吧~~

其他

因为热统学的狗屎一样, 所以卡在 Ising 模型的理解上, 先写这么多.

凉凉

前一段时间折腾了一下美赛, 发现 MMA 如果应用得好的话, 实际上哪怕对于那些数学模型具体如何实现并不是很了解, 只要你知道在什么问题用什么 (类型) 的方法, 基本上都可以 “水” 过去.

Mathematica and MultiParadigm Data Science 这个是来自 Wolfram U 的一个笔记, 这里强烈安利里面的一些比较新的课程, 有训练的练习, 讲本, 讲稿. 不过里面的大部分课程感觉重复度很高, 且讲得比较浅, 另一部分则比较难度割裂.
Mathematica and Math Modeling 基本上就是上面的一个整理以及超级功利的一个无脑笔记.

普通质粒

凉凉实际上哪怕对于那些数学模型具体如何实现并不是很了解, 只要你知道在什么问题用什么 (类型) 的方法, 基本上都可以 “水” 过去.

用Python的组表示同感，很多时候程序的核心就是调用了某个包里的一个函数来实现某种模型的运算过程，所以我们组大部分时间就是查文档、找教程、试模型，鉴定为纯纯的API Boy（乐）

BTW，组里的编程手用的Jupyter Notebook，因为也是交互式的计算所以在各种意义上都比较像MMA。不过不要问我，我反正不会用😔

凉凉

普通质粒 Jupyter 这样的笔记本一样的类型的话有一个好处就是可以在代码里面加入非常多的文本作为注释, 并且还可以每次只更新一部分代码. 感觉还是很好用的. 感觉如果不是正经搞计算机的话很推荐用这样的方式写代码. (~~正经搞计算机谁用 Notebook 编程啊~~)

~~顺带扯皮一句, org-mode 也算是一个 Notebook 类型的东西, 也是非常的好用.~~

凉凉

网上冲浪的时候看到 MMA 13.2 版本加入了 Chat-Enabled Notebook, 于是去下了正版想要尝试一下...

(学校买的正版, 去 Wolfram 的网站验证自己邮箱 (@mails.ucas.ac.cn) 就好了. ~~虽然一开始还是用的学生版... 并且旧的激活方法也能用.~~)

结果发现还是要调用 ChatGPT 的 API... 也就是说, 学校能不能再顺带买一下 OpenAI 的 API, 搓手...

Image description

(一个奇怪的地方是, 在之前用盗版的时候, 还是可以直接从 File-New-Chat Enabled Notebook 里面直接新建的. 估计是哪里卡 bug 了, 现在只能从开始界面新建...

凉凉

简单的 MMA 数据处理

获取数据

祝您实验一切顺利
祝您数据保存成功

导入数据

Mathematica 可以帮忙导入大多数的常见数据, 并且还是自动识别的:

Import["/path/to/your/data"]                 (* 自动识别 *)
Import["/path/to/your/data", "CSV"]          (* 手动声明 *)

但是有时候可能会需要检查一下 (防止自动识别出错/数据里面有问题/你比较幸运). 通常需要检查的内容:

第一行 (前几行) 是不是正确识别了:

dataset[[1;;3]]       (* 查看前 3 行数据 *)

中间的数据是否读得合理:

RandomSample[dataset, 5]      (* 随便挑 5 行数据看看 *)

筛选是否存在有问题的数据, 不过一般也不会这么倒霉吧... ~~还请对自己的实验数据自信一点.~~
这个时候可以使用 Select 之类的函数.

当然, 最简单的做法就是把数据画出来看看, 比如:

ListPlot[ #[[{1, 3}]]& /@ data ]    (* 从 data 中挑选第 1, 3 项作为 x, y 绘制点图 *)
ListLinePlot[datRT]                 (* 用 datRT 的数据来绘制线, datRT 中的元素类似于 {x1, y1} 这样 *)

(注: 画玩之后可以把鼠标放在图上看看点的信息)

数据拟合

假设您手上有一堆数据点 dat = {{1, 2}, {2, 4}, ...}

线性拟合: lmf = LinearModelFit[dat, x, x], 对于得到的结果, 通过 Normal[lmf] 来得到标准的表达式形式.
拟合一个表达式: FindFit[dat, a * x + b, {a, b}, x]
但是可能需要在一个区间里面进行拟合: FindFit[Select[xMin < #[[1]] < xMax &] @ dat, fitModel, fitParameters, fitArg].
比如可以参考下图:

总之对于 Mathematica 在 1 行之内能够实现功能的代码都还算是它的长处.

画图导出图片

Export["/path/to/export/file", plt, "PDF"] 导出图片
Show[{plt1, plt2, plt3}] 同时绘制多张图表在同一个画布上
一些相关的注意点:
- Show 函数会默认使用第一个图的参数作为自己绘图的参数, 这个时候往往会忽略后面图的参数, 需要的话可以改变图的顺序, 不过最合理的做法就是在 Show 里面加参数, 比如: Show[{...}, PlotLabels -> "标题"] 之类的.
- 绘图范围可以通过 PlotRange 来修改, 但是往往可以无脑加上 PlotRange -> All 参数来自动设置.
想让图更加正式, 就在绘图的时候加上 PlotLabels, AxesLabel 等等参数, 不过那样就会让绘图代码变得比较膨胀...

其他

把上面的两个拟合的曲线计算交点: Solve[(a * x + b /. fit1) == (a * x + b /. fit2), x], 然后往图上用 Point 绘制交点, 就是一份还算能用的实验报告图了. 感觉还行就这样了吧. 欢迎有闲情的同学来修改代码使其更加智能 (比如自动识别拟合区间之类的)

ProfessorX

凉凉这算是直播软物质作业吗（

凉凉

凉凉更加详细的内容可以看: Metropolis Hastings Algorithm (li-yiyang.github.io).
包含 ~~不靠谱的~~ 数学解释和代码实现与仿真结果.

凉凉

Ising Model MCMC 模拟

注: 这个的理论部分可以在软物质物理或者计算物理课程中学到, 如果你想要提前学的话, 可以去先修计算物理或者选一门软物质物理. 好处就是你的软物质物理的报告可以直接无缝衔接综合物理实验 II 的报告.

对实验给的程序的额外说明

如果能够用老师给的 JRE 安装并运行程序, 请忽略下面的补注说明
下面的说明仅仅针对于那些没法运行程序, 以及没有 Windows 系统 (macOS, Linux), 以及觉得现在还用 IE 有些太抽象了, 并且不喜欢每次开机都提醒你 JRE 版本过低需要更新的人
老师给的代码非常的老旧 (用的是被抛弃的 Java Applet 绘制 GUI), 所以哪怕你拥有最新版本的 JDK, 你可能还是不能使用, 因此, 你需要用 JDK 8 (还是 JDK 9) 以前的版本, 以下是一些可能的安装渠道:
- 你可以使用 Temurin 8, 一个在维护的 JDK 8, 你可以在:
- Eclipse Temurin™ Latest Releases
  随便选一个是你电脑操作系统的 JDK 即可
- adoptium/temurin8-binares (github)
- brew install temurin8 (macOS)
- 或者任意一个 JDK 8 都可
- 记得把 JDK 的环境变量添加到你的环境变量中:
```
   # macOS 或者 Linux
   export JAVA_HOME=$(/usr/libexec/java_home -v 1.8)

   echo $JAVA_HOME # 来检查你的变量是否设置正确
```
- 设置完毕后运行 appletviewer IsingApplet.html 即可得到结果, 效果图大概如下:

Image description

注: 可以观察的现象: 高温, 低温, 相变温度点的 Ising 模型的形态 (老师给的程序也只能看这个)
但是如果是软物质的话, 可以观察稳定所需要的 MC 步数, 稳定的能量, 如何判断稳定, 如果计算接受率, 如何计算热容, 如何计算能量, 磁矩, 以及其他的各种物理性质之类的.

MCMC: Markov Chain Monte Carlo Algorithm

Monte Carlo 算法相比大家应该都知道, 不过就是通过随机采样来通过统计的方式来解决某些问题嘛.

但是和用 Monte Carlo 投点法求圆周率这样简单的问题不同, 在投点法中, $P(落在圆内)$ 的概率是非常容易得到, 从而可以用来计算 $\pi$ 这个值的. 但是在大多数物理/数学问题中, 你可能不太能够找到一个直接的构造来找到满足这个分布的 “投点” 算法.

于是在这里就有一个叫做 Metropolis 算法的东西, 通过 Markov 链的方式计算得到 “投点” 对应的采样点的算法.

Metropolis 算法用简单的伪代码来说就是:

选择一个初始状态
计算一个随机游走, 得到下一个可能的状态:
- 计算下一个状态可能存在的概率 $p(E) = \mathrm{e}^{- \frac{E}{k_{\mathrm{B}} T}}$,
- 若存在 $p < p(E)$, 则更新当前状态记录, 并重复 2 步骤
- 若不存在 $p > p(E)$, 则认为当前状态保持不变, 并重复 2 步骤

注: 具体的代码应该是非常容易写的, 你完全可以自己写一个来替代掉老师给的代码. 下面给了一个 Python 的粗糙代码, ~~你可以修修改改用做自己的软物质大作业~~:

from math import exp
import random

class ising:
    def __init__(self, row, kT) -> None:
        """没有外场, 外场自己加..."""
        self.row, self.col = row, row
        self.kT  = kT

        # 注: 这里用 numpy 可以加速很多的计算,
        # 但是实际上用 C/C++ 之类的, 会更加的快
        # 一个提示是在老师给的代码里面有 C++ 的程序,
        # 你可以尝试直接用那个程序, 但是没有图形化输出
        self.spins = [[1 - 2 * random.randint(0,2) for _ in range(self.col)]
                      for _ in range(self.row)]

    def metropolis_step(self):
        for row in range(self.row):
            for col in range(self.col):
                dE = 2 * self.at(row, col) * sum(self.near(row, col))
                rand = random.random()
                p = exp(- dE / self.kT)

                if dE < 0 or p < rand:
                    self.flip_spin(row, col)
                    # 此处应当调用更新能量和更新磁矩的函数
                    # 比如:
                    # + self.energy += dE
                    # + self.energy -= 2 * self.at(row, col)       

    # 辅助用的函数                    
    def at(self, row, col):
        """在 row, col 处的自旋反向"""
        return self.spins[row][col]

    def near(self, row, col):
        """周期性边界条件确定的周围的自旋"""
        r, c = self.row, self.col
        return [self.at((row - 1) % r, col),
                self.at((row + 1) % r, col),
                self.at(row, (col - 1) % c),
                self.at(row, (col - 1) % c)]

    def flip_spin(self, row, col):
        """翻转 row, col 处的自旋."""
        self.spins[row][col] *= -1

    # def 此处应有计算能量和计算磁矩的函数,
    # 但是想必这些都非常简单, 大家都不乐意看
    # 就略了吧

注: 原始代码来自我的 Lisp 程序 (见原始网页, 对 Python 并不是非常熟, 可能有错误, 最终结果如下图所示

(啊, 这个 gif 有点糊...)

注: 或者也可以参考 Mathematica 的实现, Mathematica 画图虽然慢一点, 但是很省事, 可以见论坛链接凉凉

注: 一个比较神奇的是, 这代码可能比我年龄还要大...

Image description

凉凉

ProfessorX 其实是写作业的时候发现代码不方便可视化输出 🥲, 于是换成了 MMA.
~~不过要比性能的话, 还是换其他的/改多线程/抓一个计算机系的比较靠谱~~

凉凉

难绷, 帮人尝试使用学校账号安装 MMA, 结果网络卡死根本没法验证, 于是直接 “学生版” 走起 🤣👉.
貌似 Windows 上的 360 对 MMA 颇有意见, 一路安装下来一直在报错 💦.

凉凉

一些简短的 Mathematica 代码的例子: (没空写长文字了)

(* 施密特正交化 *)
dot[e1_, e2_] := Integrate[e1*e2, {x, -1, 1}];
unify[expr_] := expr/Sqrt[dot[expr, expr]];
Fold[Function[{base, e}, 
  Append[base, unify[e - Total[dot[e, #]*# & /@ base]]]], {}, {1, x, x^2, x^3}]

(* Results: {1/Sqrt[2], Sqrt[3/2] x, 3/2 Sqrt[5/2] (-(1/3) + x^2), 5/2 Sqrt[7/2] (-((3 x)/5) + x^3)} *)

对 $(-1, 1)$ 上的 $1, x, x^{2}, x^{3}$ 进行正交化. 除了数学上的定义以外 (相信大家不用看线性代数都还记得这个是个啥), 在代码逻辑上的核心函数是: Fold: 其作用是将一个列表 (第三参数), 以第二参数为初始值, 不断递归调用:

Fold[f, init, {a, b, c}]  (* => f[f[f[init, a], b], c] *)