第二章 概率分布
本章中将介绍几种重要且常用的概率分布。
三大离散分布
二项分布
- 做n次实验,每次实验都有两个结果(比如说成功和失败),成功概率是p,变量x是成功的次数。
(我发现我不会用Latex敲公式)
因此二项分布有两个参数n和p,变量是成功次数x.
- 二项分布的期望E(X) = np,方差V(X) = np(1-p),均值大于方差,离散程度较小
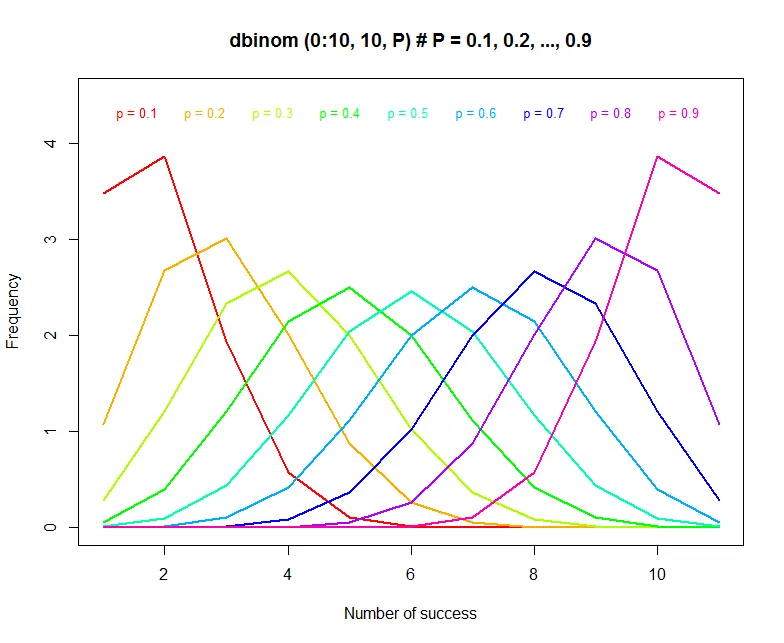
- 可以使用R大概地画出二项分布的概率密度函数。可以看出只有p是0.5的时候概率密度函数才是对称的。
binomial.PDF = dbinom(0:10, 10, 0.5)
plot(binomial.PDF * 10, type = 'l', ylim = c(0, 4.5),
xlab = "Number of success", ylab = "Frequency",
main = paste('dbinom (0:10, 10, P) # P = 0.1, 0.2, ..., 0.9', sep = '' ''))
for (i in seq(0.1, 0.9, by = 0.1)) {
binomial.PDF = dbinom(0:10, 10, i)
lines(binomial.PDF * 10, type = 'l',
col = rainbow(9)[i*10], lwd=2)
legend(-0.3 + 11 * i, 4.5,
paste('p =', i, sep = '' ''),
text.col = rainbow(9)[i * 10],
box.lty = 0, cex = 0.8) }
泊松分布
- 只有一个参数$\lambda$,变量x为事件发生的次数。一般来说泊松分布被用来描述一个小概率事件的发生次数,在有些时候泊松分布和二项分布的概率密度函数比较像,特别是在n比较大,p比较小时。这个时候如果用二项分布进行拟合的话计算量比较大(因为要算那个庞大的组合数),就不如采用泊松分布进行拟合。在后面的“广义线性模型”部分中(如果我真的能坚持到写到那儿),我们将可以使用这三大离散分布构建因变量的回归模型。
- 泊松分布的E(X) = V(X) = $\lambda$,均值等于方差,离散程度适中
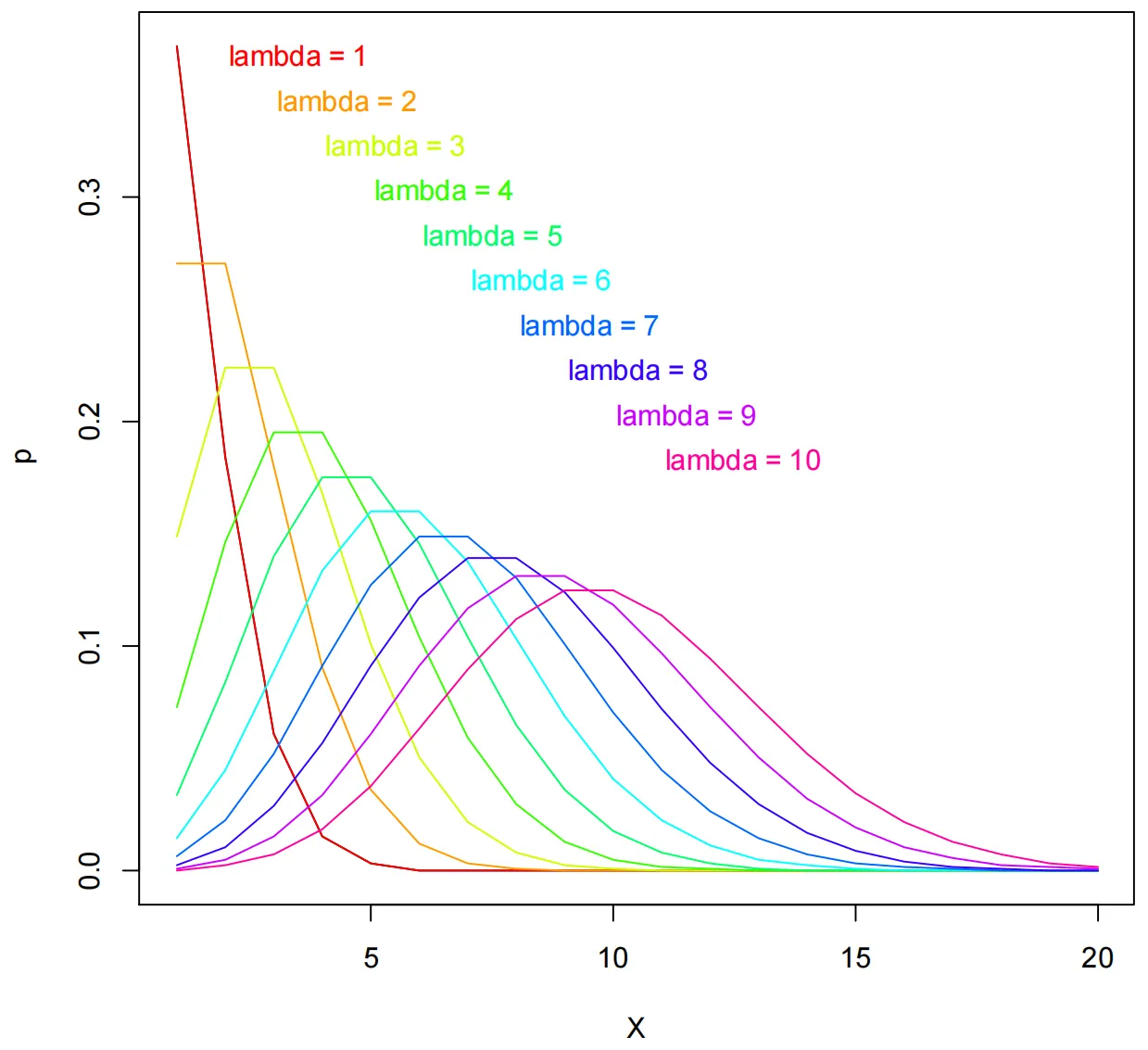
- 同样地,我们可以用R大概地画出泊松分布的概率密度函数。
lambda <- 1
poisson.d <- dpois(seq(1,20), lambda)
plot(poisson.d, xlab = 'X', ylab='p', type='l')
for (lambda in 1:10){
poisson.d <- dpois(seq(1,20), lambda)
lines(poisson.d, type = 'l',
col = rainbow(10)[lambda])
legend(lambda, 0.4-lambda/50,
paste('lambda =', lambda, sep=' '),
text.col = rainbow(10)[lambda],
box.lty = 0, cex = 0.8)}
负二项分布
- 与二项分布类似,同样是做只有两个结果,成功概率为p的实验,但是不管一共做了几次,而是只关心总的失败次数r,变量x是在失败r次的时候成功的次数。
- 负二项分布的E(X) = rp/(1-p), V(X) = rp/(1-p)2 ,均值小于方差,离散程度较大。
我着重标出了三种分布离散程度的差异。其实在生物研究中进行统计学的工作不需要完全理解这个分布到底在数学上是什么意思,只需要知道什么时候用哪个分布即可。而对于是离散变量的数据,判断应该用哪个分布进行拟合的标准很多时候就是用样本均值和方差的比较来确定。因此了解这三个分布的离散程度的差别是最主要的内容。
连续分布
连续分布中将会面对更复杂的概率密度函数,但事实上做科研根本不需要知道这些密度函数怎么写,只需要知道这些分布之间的关系,以及什么时候用哪个分布就足够了。
正态分布
我觉得正态分布可以说是最最常用的分布了,其本质上是一个钟型曲线e-x2 经过将x减去均值$\mu$再除上方差$\sigma$2 ,再乘上归一化系数的过程得到的概率密度分布。神奇的是自然界有许多现象都符合这种中间多两边少的分布情况,以至于我们可以用正态分布或近似的正态分布进行假设检验、方差分析等等操作。
- Z统计量。对于一个服从正态分布的变量x,如果我对其减去均值除上标准差,它就变成了一个标准化了的x,从而也就服从N(0, 1)。这种“标准化”的思想非常重要,当我们想要比较不同x之间的差距(比如一个同学在SAT中的得分和另一个同学在ACT中的得分),由于评价体系不一样、总分不一样,不能直接拿绝对分数进行比较,然而由于参加考试的同学的成绩分布是服从正态分布的,因此可以将两个分数都标准化后再进行比较,这样就可以知道哪个同学的分数更好。这与后面进行假设检验时的逻辑是相同的。
- 中心极限定理:任何一种分布的均值的分布是正态分布。大概是这么个意思,但这样说不太严谨,应该说,无论原始分布是什么,随着样本量N的增大,抽样得到的均值的分布逐渐趋于正态分布。而均值的方差就是前文中所提到的标准误(standard error)。中心极限定理在t-检验中非常有用,因为有些时候的t-检验是对样本均值的检验,而t-检验又需要正态性的前提条件,中心极限定理就使得正态性的条件天然满足。
卡方分布
卡方分布拥有极其复杂的概率密度函数,我们不需要知道是什么。我们只需要知道卡方分布只有一个参数,即它的自由度(Degree of freedom),而正态分布的平方服从卡方分布,如Z统计量的平方服从自由度为1的卡方分布。而数据的方也是服从卡方分布,自由度为N-1.
- 卡方分布的E(X) = DF, V(X) = 2×DF
F分布
F分布是正态分布的两个方差之比,也是两个卡方分布各自除以各自自由度之后的比。因此F分布有两个参数,即两个卡方分布的自由度。了解到这里就足够了。由于F分布的这个性质,通过F-检验可以检验两个正态分布的方差是不是有显著差异(即F值是不是显著不为1)。
为了便于大家理解,这里还是将F分布的概率密度函数图像展示出来。在将来做F-检验时也更好理解是如何判别的。
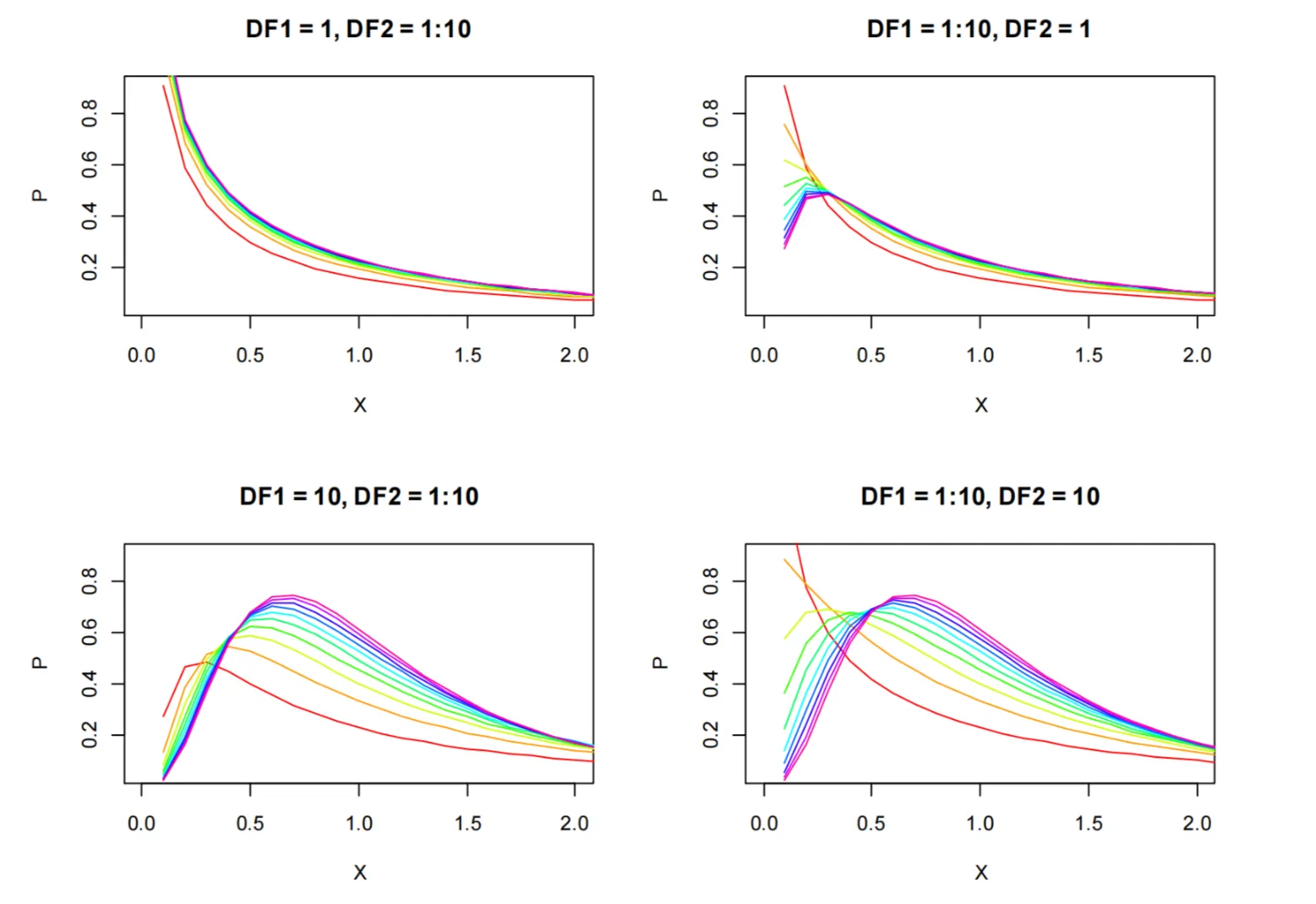
所使用的R代码如下。
X = seq(0.1, 3, length=30); Y = df(X, 1,1)
par(mfrow=c(2,2))
plot(X, Y, type='n', xlab = 'X', ylab = 'P', xlim=c(0,2), main="DF1=1, DF2=1:10")
for (i in 1:10) lines(X, df(X, 1, i), col=rainbow(10)[i])
plot(X, Y, type='n', xlab = 'X', ylab = 'P', xlim=c(0,2), main="DF1=1:10, DF2=1")
for (i in 1:10) lines(X, df(X, i, 1), col=rainbow(10)[i])
plot(X, Y, type='n', xlab = 'X', ylab = 'P', xlim=c(0,2), main="DF1=10, DF2=1:10")
for (i in 1:10) lines(X, df(X, 10, i), col=rainbow(10)[i])
plot(X, Y, type='n', xlab = 'X', ylab = 'P', xlim=c(0,2), main="DF1=1:10, DF2=10")
for (i in 1:10) lines(X, df(X, i, 10), col=rainbow(10)[i])
最后
有些时候我们需要用R代码化想要分布的PDF、CDF,或是得到某个概率值对应的x值,或是x值对应的频率等等(我也不知道什么时候会用到这些东西但码着总是会有用的),这里将提供一些R代码可以实现与概率分布相关的功能。
# Normal distribution
dnorm(seq( -3, 3, by = 0.1), mean = 0, sd = 1)
pnorm(seq( -3, 3, by = 0.1), mean = 0, sd = 1)
qnorm(seq( 0.1, 0.9, by = 0.1), mean = 0, sd = 1)
rnorm(10, mean = 0, sd = 1)
# 'dnorm' gives the pdf
#'pnorm' gives the cdf
#'qnorm' gives the quantile function
#'rnorm‘ generates random deviates
dbinom(x, N, p) # Binomial distribution
pbinom(x, N, p)
qbinom(q, N, p)
rbinom(n, N, p)
rchisq(100, df = 3) # chi square distribution
runif(x, min, max) # Uniform distribution
rnbinom(10, mu=3, theta=2) # Negative binomial distribution
rpois(x, lambda) # Poisson distribution
rgamma(100, shape = 3, scale = 2) # Gamma distribution
rweibull(100, shape = 3, scale = 2) # Weibull distribution
# F distribution
df(x, df1, df2, log = FALSE)
pf(q, df1, df2, lower.tail = TRUE, log.p = FALSE)
qf(p, df1, df2, lower.tail = TRUE, log.p = FALSE)
rf(n, df1, df2)
By the way, 这三大离散分布和正态分布都属于指数族分布,对服从指数族分布的因变量才可以用广义线性模型构建回归模型。
一些基础的概念大概到这里就这么多,下面将开始从假设检验、方差分析等开始,展示一些真正实打实在科研中用得到的统计分析方法。